Carl Friedrich Gauss (1777-1855)
Fue niño prodigio de clase obrera que llegó a ser el mejor matemático de su tiempo, fue matemático alemán llamado “el príncipe de las matemáticas”, podría decirse que fue gracias a la visión y el mecenazgo de Carlos Guillermo Fernando duque de Brunswick-Wolfenbüttel que pudo desarrollar su fenomenal talento. En 1791, el duque ofreció pagar los estudios universitarios de Gauss, quien entonces tenía 14 años.
El noble estaba convencido de que una población bien educada era la base del éxito comercial de Brunswick y siempre estaba pendiente de los estudiantes sobresalientes.
Gauss era uno de ellos. A los 15 años, detectó un patrón extraordinario escondido entre los números primos, uno de los mayores misterios en las matemáticas en ese momento.
A los 19 años, descubrió una hermosa construcción de una figura regular de 17 lados -un heptadecágono- utilizando solo una regla y un compás, algo que durante 2.000 años se había pensado imposible.
Desde el tiempo de la antigua Grecia hasta que Gauss hizo esta figura que se pensaba que no existía, solo se sabía de las reglas para construir triángulos regulare, cuadrados, pentágonos y una figura de 15 lados iguales usando sólo una regla y un compás, además de todas las figuras que lindan ese número de lados. Esa edad, tal vez para mantenerse al día con sus múltiples avances, comenzó a llevar un diario matemático. Las entradas empiezan en 1796 y la última tiene la fecha de 9 de julio de 1814.
En las 19 páginas de uno de los documentos más preciosos de la historia de las matemáticas están registrados brevemente 146 resultados como...
30 de marzo, Brunswick: Los principios de los que depende la división del círculo y la división geométrica del mismo en 17 partes.
27 de junio, Gotinga: Una nueva prueba del teorema áureo todo a la vez, desde cero, diferente y no poco elegante.
10 de julio: Todo número entero positivo puede expresarse como suma de como mucho tres números triangulares
Aunque estaba tan emocionado con este último descubrimiento que realmente lo que escribió en su diario, más tarde, recopiló muchas de estas entradas de diarios sobre las propiedades de los números en su primer libro, publicado en 1801, "Disquisitiones Arithmeticae", dedicado al generoso duque.
En él -entre otras cosas- estaba el fundamento para una nueva rama de las matemáticas, la teoría de los números, con siete sellos
Gauss esperaba que su obra lo hiciera notable en Francia, el epicentro de las matemáticas en Europa. Sin embargo, para su gran disgusto, no fue bien recibida por la Academia de Ciencias de París. Hasta cierto punto, él mismo tuvo la culpa.
Presentó sus ideas de una tan manera increíblemente críptica que hubo quienes describieron su tratado como un libro "sellado con siete sellos".
No obstante, un matemático francés le escribió:
"Su Disquisitioned Arithmeticae ha sido objeto de mi admiración y mi estudio durante mucho tiempo.
"El último capítulo de este libro contiene, entre otras cosas, el hermoso teorema sobre la ecuación 4 (x ^ n-1) / (x-1) = y ^ 2 + -nz ^ 2; Creo que se puede generalizar (...)
"Me tomo la libertad de someter este intento a su juicio, persuadido de que no desdeñará ayudar, con su consejo, a un aficionado entusiasta en la ciencia que usted ha cultivado con tan brillante éxito".
Fue el comienzo de una correspondencia que iba a tener consecuencias más allá de las matemáticas.
En noviembre de 1806, su protector, el duque Fernando, resultó herido de muerte en una batalla contra el ejército de Napoleón.
El estado de Hannover quedó bajo el control de Napoleón y los profesores se vieron obligados a pagar un impuesto al gobierno francés de 2.000 francos, una pequeña fortuna en el momento,
Gauss se negó, poniéndose en gran peligro.
Pero el misterioso Monsieur Le Blanc usó su influencia para asegurarse de que no le ocurriera nada malo al joven y brillante Gauss.
Fue solo cuando Gauss intentó agradecérselo que descubrió su verdadera identidad: Monsieur Le Blanc era en realidad una mujer llamada Sophie Germain.
La extraordinaria matemática que mintió para que la tomaran en serio y ayudó a resolver "una de las ecuaciones más difíciles" de la historia
"Por temor al ridículo que acompaña a una estudiante, previamente he tomado el nombre de M. LeBlanc al comunicarle aquellas notas que, sin duda, no merecen la indulgencia con la que usted ha respondido", le explicó Germain.
Gauss le respondió expresando su asombro ante el giro de los acontecimientos:
"Los encantos cautivadores de esta sublime ciencia son revelados solo a aquellos que tienen el coraje de profundizar en ella.
"Pero si una mujer, que por su sexo y nuestros prejuicios encuentra infinitamente más obstáculos que un hombre para familiarizarse con problemas complicados, logra vencer estos obstáculos y penetrar en las partes más oscuras de ellos, sin duda debe tener el coraje más noble, talentos extraordinarios y genio superior"
Gauss había hecho la mayor parte del trabajo para Disquitiones mientras el duque Fernando le pagaba para que se dedicara a la Astronomía, específicamente a trazar los caminos de varios cuerpos celestes: primero Ceres, luego Pallas, luego Juno.
En aquellos días, explorar el cielo nocturno era considerado como una ciencia real: no así el estudio de matemáticas, particularmente algo tan abstracto como las propiedades de los números.
Pero en noviembre de 1806, con su patrón muerto, Gauss se vio obligado a buscar un trabajo.
Un cargo académico tal vez habría sido la opción obvia, pero él le tenía "una verdadera aversión a la enseñanza", pues los estudiantes con "talentos únicos no quieren que los eduquen mediante cursos magistrales, sino aprender por sí mismos".
Pero nadie iba a pagarle por investigar, así que Gauss aceptó un puesto como director del Observatorio en Göttingen, una pequeña ciudad universitaria en Baja Sajonia, ahora en Alemania.
Su personalidad era contradictoria, era un hombre frío y concentrado en su trabajo, un perfeccionista que no admitía que sus trabajos fuesen publicados antes de que estuviesen completamente revisados. Sobre su temprana genialidad (él mismo solía decir que había prendido a contar antes de hablar). Cuando tenía 10 años de edad, estando en clase de aritmética, su profesor propuso el problema de sumar los primeros cien números 1+2+3…+100.
Mientras todos los alumnos se desgastaban con la interminable suma, Gauss descubrió el camino rápido, escribió un solo número en su pizarra, ante la perplejidad del profesor, luego el profesor le regaló un número de aritmética que Gauss leyó (y corrigió rápidamente).
Fue quién demostró el Teorema Fundamental del Algebra.
Gauss alcanzaba elevadas cotas de razonamiento, invención e innovación. Gauss tuvo un problema similar con Ceres: hubo muchas mediciones sobre su paradero antes de que desapareciera, pero no había indicios sobre su verdadera posición.
Lo que descubrió fue que, si trazaba la posición real de Ceres en el cielo nocturno con las observaciones inexactas de su paradero, obtenía una curva en forma de campana.
Esto es lo que se conoce como la función gaussiana o campana de Gauss.
Gauss hizo además aportaciones fundamentales a la astronomía, la geodésica y a varias ramas de la física como el magnetismo y la óptica. Pero su gran amor era la matemática pura. En una carta a un amigo escribió: "La matemática es la reina de las ciencias y la teoría de números es la reina de la matemática".
Las ideas de Gauss también arrojan luz sobre la correlación estadística.
El método que Gauss inventó para recuperar al planeta perdido te ayuda a responder estas preguntas. Por eso es la base de la medicina moderna. Pero en noviembre de 1806, con su patrón muerto, Gauss se vio obligado a buscar un trabajo.
Un cargo académico tal vez habría sido la opción obvia, pero él le tenía "una verdadera aversión a la enseñanza", pues los estudiantes con "talentos únicos no quieren que los eduquen mediante cursos magistrales, sino aprender por sí mismos".
Pero nadie iba a pagarle por investigar, así que Gauss aceptó un puesto como director del Observatorio en Göttingen, una pequeña ciudad universitaria en Baja Sajonia,
Ahora en Alemania. Su tesis doctoral (1799) versó sobre el teorema fundamental del álgebra (que establece que toda ecuación algebraica de coeficientes complejos tiene soluciones igualmente complejas), que Gauss demostró.
Pitágoras
Autor: Ruiza, M., Fernández, T. y Tamaro, E.
Editorial: Biografías y Vidas.
Fuente: https://www.biografiasyvidas.com/biografia/p/pitagoras.htm
Nació en Jonia, en la isla de Samos hacia el año 572 A.C y muere por el año 500 A.C, fue un filósofo y matemático griego, se casó con Teano uno de sus discípulos; vivió en Mileto, fenicia y Egipto, en éste último estudio geometría y astronomía; luego se trasladó a Babilonia.
Fundo la escuela de Pitágoras en Crotona (Italia), allí se enseñó la importancia de los números para poder entender el mundo. De igual manera se atribuye a él, haber transformado las matemáticas mediante la formulación abstracta de resultados al realizar aportes como la división de los números naturales en pares e impares, divide la aritmética como ciencia, relacionan la música con las matemáticas; los pitagóricos realizan la primera división, conocían las medidas y proporciones aritméticas, geométricas y armoniosas. El aporte más importante que se puede mencionar es el Teorema de Pitágoras que no dice que en un triángulo rectángulo, el cuadrado sobre la hipotenusa (lado más largo) es igual a la suma de los cuadrados de los catetos (lados más cortos).
Los pitagóricos consideraban la música un instrumento para purificar el alma, debido a su doctrina filosófica donde la música y las matemáticas desempeñaban un papel muy importante, que hacía relación entre el orden cósmico y lo moral donde el alma era la armenia del cuerpo; por medio de Platón muchas sus teorías o concepciones filosóficas se convierten en temas recurrentes de la filosofía occidental, también se incorporó la armonía y proporción a la música y las artes.
Abstract
Pythagoras: He was born in Ionia, on the island of Samos around 572 BC. and died around 500 BC, he was a Greek philosopher and mathematician. I founded the Pythagorean school in Crotona (Italy), where I taught the importance of numbers to understand the world; they did the first division, they divided the natural numbers into odd and even numbers, but perhaps one of the biggest contributions is the Pythagorean theorem related to the right triangle.
Isaac Newton
(1643 – 1727), Físico, alquimista, matemático- astrónomo- inventor de las leyes de newton – calculo diferencia y calculo integral.
Matemático inglés, cuando el matemático Isaac Newton nació, fue en un tiempo en el que se predecía que había una guerra civil y además el fin del mundo, era un bebe bastante pequeño donde lastimosamente se creía que no viviría por mucho, sin embargo logro salir adelante para empezar su padre murió y su madre a la edad de 3 años lo dejo con sus abuelos por que se casó con otro hombre, generando en el abandono y la depreciación de cada uno de los integrantes de su familia evidenciándose así el acompañamiento de cada una de las etapas que tuvo que pasar de niño de acuerdo a cada una de estas situaciones fue un estudiante que se refugió en los libros y en su lugar preferido que fue la biblioteca, se dedicó a ser el uno de los mejores lectores pero comentado así, y criticado por sus docentes por ser un estudiante autodidacta mediocre.
Newton estudiaba cada uno de los matemáticos que dejaron huella y que habían hecho cada uno de sus aportes a la ciencia, donde comentaba Aristóteles y Platón son mis amigos, pero mi mejor amiga es la lectura y la observación donde cada una de ellas tomaba un papel importante a la hora de rectificar cada uno de los avances y experimentos que Newton quería comprobar por medio de experiencias propias como realizar el proceso de experimentación con la aguja sin punta e insertársela en el ojo, generando así las posibles respuestas que se daban y relacionándolas con la óptica en el que se presentó uno de sus aportes principales y por los que el intento de todas las formas claras dejarlo claro con sus experiencias propias, he aquí donde aparece la Teoría de la luz comentada y estudiada por el mismo.
Newton en una de sus etapas hubo una en el que su madre enferma, el decide acompañarla en su proceso de enfermedad en aquella situación, se tomó el trabajo de estudiar la alquimia campo de la química donde lo llevo a descubrir el mercurio filosófico para descomponer el mercurio y volver a reconstruir con procesos que lo llevan a mantenerlo en la misma composición.
Sin embargo, existen disputas con el Físico Leibniz donde cada uno defendía sus teorías en el cálculo infinitesimal en el que se nombraba que las ecuaciones se podían escribir de forma física; al observar cada una de estas situaciones Newton decidió publicar sus apuntes que defendían cada una de las teorías en las cuales él había estudiado y experimentado.
Newton se considera en la historia como el papa de la ciencia moderna, además de todos sus talentos encontró su parte religiosa y político tomando papeles importantes en la sociedad mostrando en su estado de salud un desmejoramiento en su parte mental por el uso excesivo del mercurio generando así un colapso mental, es decir un bajonazo en su proceso académico y laboral.
El predijo en el año 1764 que el fin del mundo va a ser en el año 2062 antes de Cristo, nombra también una restauración de Israel con la siguiente frase del libro de la APOCALIPSIS citado así:
Efectivamente los judíos fueron restaurados en el año de 1948.Newton murió a los 84 años, filósofo natural sentó las bases del movimiento y la teoría de la gravedad, y dejo como enseñanza que las matemáticas y la teología son un solo proyecto.
Abstract
(1643 - 1727), Physicist, alchemist, mathematician- astronomer- inventor of Newton's laws - difference calculus and integral calculus.
English mathematician, when the mathematician Isaac Newton was born, it was at a time when it was predicted that there would be a civil war and also the end of the world, he was a fairly small baby where unfortunately it was believed that he would not live for long, however he managed to get out forward to begin with his father died and his mother at the age of 3 left him with his grandparents because she married another man, generating in the abandonment and depreciation of each of the members of his family thus evidencing the accompaniment of each one of the stages that he had to go through as a child according to each of these situations was a student who took refuge in books and in his favorite place which was the library, he dedicated himself to being one of the best readers but commented like this , and criticized by his teachers for being a mediocre self-taught student.
Newton studied each of the mathematicians who left their mark and who had made each of their contributions to science, where Aristotle and Plato commented are my friends, but my best friend is reading and observation, where each one of them took a role important when rectifying each of the advances and experiments that Newton wanted to verify through his own experiences, such as carrying out the experimentation process with the blunt needle and inserting it into the eye, thus generating the possible answers that were given and relating them to the optics in which one of his main contributions was presented and for which the attempt in all clear ways to make it clear with his own experiences, here is where the Theory of light appears, discussed and studied by him.
Newton in one of his stages there was one in which his sick mother, he decides to accompany her in her disease process in that situation, he took the trouble to study the alchemy field of chemistry where it led him to discover the philosophical mercury to decompose the mercury and rebuild with processes that lead to keep it in the same composition.
However, there are disputes with the Physicist Leibniz where each one defended his theories in the infinitesimal calculus in which it was named that the equations could be written in a physical way; Upon observing each of these situations, Newton decided to publish his notes that defended each of the theories in which he had studied and experimented.
Newton is considered in history as the pope of modern science, in addition to all his talents, he found his religious and political part taking important roles in society showing in his health a deterioration in his mental part due to the excessive use of mercury generating thus a mental collapse, that is to say a downturn in their academic and work process.
He predicted in the year 1764 that the end of the world will be in the year 2062 before Christ, he also names a restoration of Israel with the following phrase from the book of APOCALYPSE quoted like this:
"The ruin of the ungodly nations, the end of weeping and all troubles, the return of the Jews from captivity and their setting up of a flourishing and eternal kingdom"
Indeed, the Jews were restored in 1948. Newton died at 84 years old, a natural philosopher laid the foundations of the movement and the theory of gravity, and taught that mathematics and theology are a single project.
Leibniz
Gottfried Wilhelm Von
Leibniz nació en 1646 Leipzig, Alemania y falleció en Hannover en 1716, fue un
Filósofo y Matemático Alemán. Estudió Matemáticas en la Universidad de Jena, en
1672 inventó una máquina capaz de realizar las operaciones de multiplicación, división
y extracción de raíces cuadradas, así como la elaboración de las bases del cálculo
infinitesimal.
Sus contribuciones en el
campo del cálculo infinitesimal fueron notorias, trabajos en los que logró
independencia de los trabajos de Newton, así como en el ámbito del
análisis combinatorio, introdujo la notación actualmente utilizada en el
cálculo diferencial e integral. En su juventud intentó buscar un lenguaje
perfecto que reformara toda la ciencia y permitiese convertir la lógica en un
cálculo. Introdujo notaciones como el signo integral que era una S alargada que
viene del latín “suma” y la d de la palabra latina “diferencia” que se utiliza
para los cálculos diferenciales. Contribuyó a la definición de las
entidades matemáticas que llamamos “infinitesimales” y a definir sus
propiedades algebraicas, Leibniz estableció que la complejidad del
razonamiento humano podría traducirse al lenguaje de los cálculos, y que, una
vez comprendidos podían ser la solución para resolver diferencias de opinión y
argumentaciones. De lo anterior se deriva que fue reconocido como el lógico más
significativo de la época.
Abstract
Leibniz was a German Philosopher and Mathematician. He studied Mathematics at the University of Jena, in 1672 he invented a machine capable of performing the operations of multiplication, division and extraction of square roots, as well as the elaboration of the bases of the infinitesimal calculus. His contributions in the field of infinitesimal calculus were notorious, works in which he achieved independence from Newton's works, as well as in the field of combinatorial analysis, he introduced the notation currently used in differential and integral calculus. He introduced notations such as the integral sign that was an elongated S that comes from the Latin "sum" and the d of the Latin word "difference" that is used for differential calculations. He contributed to the definition of the mathematical entities that we call "infinitesimals" and to define their algebraic properties, established that the complexity of human reasoning could be translated into the language of calculations, and that, once understood, they could be the solution to resolve differences of opinion and arguments.
René Descartes
“Cogito Ergo Sum” (Pienso, luego existo)
Filósofo y matemático nacido en La Haye, Francia en 1596. Iniciador del racionalismo, se propuso construir una nueva forma de pensar, poniendo por encima la razón, influyendo en la metodología de las matemáticas; y por causa de sus ideas fue perseguido.
Aportes a las Matemáticas:
Sus principales aportes en el campo de las matemáticas, se basan en proponer el método cartesiano, para todas las ciencias y disciplinas. Los ensayos científicos que seguían al discurso, ofrecían un compendio de sus teorías físicas, entre las que destaca su formulación de la ley de inercia y una especificación de su método para las matemáticas.
René Descartes es el padre de la geometría analítica y fue el primero en utilizar el plano cartesiano y sus coordenadas; mostró que una ecuación tiene tantas raíces positivas como cambios de signos hay en la serie de coeficientes y tantas negativas como repeticiones de signos, además dedujo que la ecuación de tercer grado se resuelve por radicales cuadráticos y estableció que una ecuación algebraica tiene varias raíces como unidades tiene su potencia mayor. También distinguió curvas geométricas y mecánicas en un plano, determinó el radio y el centro de un círculo que debe cortar la curva en dos puntos consecutivos y creó una técnica para expresar las leyes de la mecánica mediante fórmulas algebraicas.
Por último, ya ha quedado claro que aportó una infinitud de cosas a las matemáticas, pero sabiendo todo lo que Descartes hizo a lo largo de su vida, apoyando en todo momento al progreso de la ciencia, es justo decir que es uno de los filósofos que colaboró más a la humanidad con sus grandes contribuciones a los campos que fueron objeto de su estudio.
Abstract
René Descartes was a philosopher and mathematician born in La Haye, France in 1596. Initiator of rationalism, he proposed to build a new way of thinking, putting reason above, influencing the methodology of mathematics.
His main contributions in the field of mathematics are based on proposing the Cartesian method, for all sciences and disciplines. The scientific essays that followed the discourse offered a compendium of his physical theories, among which his formulation of the law of inertia and a specification of his method for mathematics stand out.

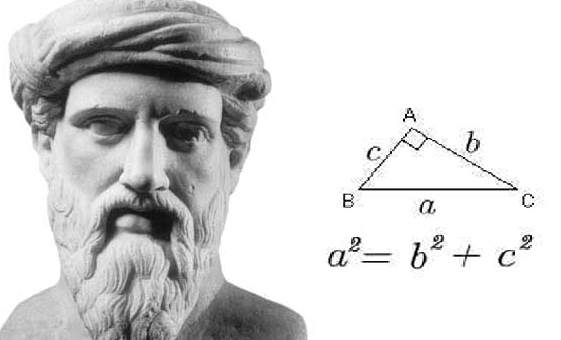



No hay comentarios:
Publicar un comentario